
暗記するのって苦手・・・

暗記って面倒くさい・・・
そう思う方は多いはず!
そこで、私なりに考えた暗記の考え方やコツについて書いていこうと思います。
書き始める前に、私の経歴について述べておくと・・・
・中学生:3年間、定期テスト学年1位/約60人
・高校生:3年間、定期テスト学年5位以内/約280人
・某国公立大学に現役で入学
・成績優秀者として大学を飛び級で卒業(3年で卒業)
という感じです。
昔から学校のテストが得意でしたが、それを支えていたのが「暗記」です。
暗記を得意になりたい方は是非続きをご覧ください!
暗記に対する考え方
暗記力 VS 発想力
「暗記」と「発想」はよく対比されますが、先に結論を言うと、
「暗記しているからこそ発想ができる」
ということです。暗記をしていないと発想することもできません。
特に数学については「発想力が大事」と勘違いしている人が多いです。
発想力が大事となる問題はごくごく一部、しかもかなり難しい問題です。
「定石の暗記」が数学の勉強です。
こういう問題がきたらこうやって解く
というパターン(定石)を覚えるのが重要です。
以下のサイトで、数学の勉強法について詳しく説明していますので、ぜひ参考にしてください!

もちろん、発想力を鍛えることは素晴らしいことですが、暗記ありきのものであるということに気をつけてください。
理解があっての暗記
では、ひたすら暗記をすればいいのか。というとそうではありません。
暗記の前提にあるのが「理解」です。
主要5科目で例を挙げましょう。
国語:意味・活用・接続も分からずに古文の助動詞を覚える
→「る・らる・まし・まほし・き・けり・らし・めり・・(中略)・・り・べし。よし、全部言えたぞ!」
主に高校で習う古文の助動詞です。種類を言えるのが大事なわけではありません。
数学:使い方・意味も分からずに公式を覚える
→「a2 = b2 + c2 – 2bccosθ 、b2 = a2 + c2 -2cacosθ、c2 = a2 + b2 -2abcosθ。よし、3つとも言えたぞ!」
余弦定理という公式ですが、そもそも3つ覚える必要がありません。文字で公式を覚えることだけに専念していると、理解を怠ってしまいます。
英語:意味も分からずに文法事項を丸暗記
→「have + 過去分詞で現在完了、be + 過去分詞で受動態、be + ~ingで現在進行形!よし、形覚えた!」
中学生で習う英文法ですが、形だけ覚えてそれぞれの意味や違いを理解していない人がいます。
理科:化学反応式をひたすら覚える
→「NaOH + HCl → H2O + NaCl、Ba(OH)2 + H2SO4 → H2O + BaSO4。全部覚えるの大変だなぁ・・・」
化学反応は法則に従って起こります。(上は2つとも中和反応の式)それらの法則を理解しなければ非効率な暗記になります。
社会:年号をひたすら覚える
→「1853年にペリー来航、1582年に本能寺の変、1932年に五・一五事件・・・」
歴史で大事なのは年号ではなく「流れ」です。そこを理解せずに年号を覚えても効果は薄いです。
どうでしょうか。今回は極端な例を挙げましたが、似たようなことに心当たりはないでしょうか。
このような「理解していないことを覚える」のは効率も効果も非常に悪いです。
ここまでをまとめると、勉強の段階は
理解 → 暗記 → 発想
となります。テストでは理解 → 暗記 までのステップを重点的に心がけましょう!
暗記の方法
ここから具体的に暗記の方法論について述べていきます。
関連させる
人間の脳は、単独で覚えるより何かと関連づけて覚えるほうが記憶に残るようにできています。
具体的な方法として以下の2つがあります。
① 語呂合わせ
最も代表的な関連手法です。1.7320508・・・(√3)という無意味な数字の羅列を「人並みにおごれや」と語呂合わせすることで覚えやすくなります。
語呂合わせは、無意味な数字/文字の羅列・順番が重要な事柄に対して唯一と言っていい対抗手段です。
覚えれないことは語呂合わせを自分で考えて覚えていきましょう。
② 周辺知識を入れる
単独の知識で覚えるより、周辺知識も知った方が覚えやすいです。
例えば、「野口英世は黄熱病の研究者」ということを覚えたいとします。
今の状態だと「野口英世ー黄熱病」というつながりしかないです。
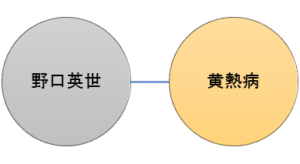
そこで、周辺知識を調べてみます。
「野口英世は幼い頃にいろりで手に大やけどを負ったが治療してもらったことで医者を志す。黄熱病で研究しているときに黄熱病で死んでしまった。金遣いが荒く、アメリカ留学のためにもらったお金を宴会に使ってしまったことがある。」
という情報を知ることができました。
こうなると、「野口英世」という1つのワードから「黄熱病」「幼少期にやけど」「死因も黄熱病」「金遣いが荒い」といった情報がリンクされ、脳は覚えやすくなるのです。
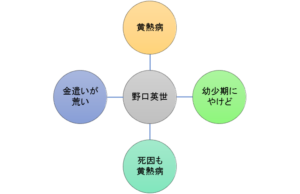
なかなか覚えられないことがあるときはネットで周辺知識を知りましょう。
アウトプットをする
「暗記」と聞くと「インプット」のイメージが強いと思います。
しかし、暗記をするためには「アウトプット」が大事です。
アウトプットをすることで脳に定着します。
以下で具体的なアウトプットの方法を書きます。
① 問題集
一般的なアウトプット方法です。数学では特に効果を発揮します。
問題集のメリットとしては以下のようなことがあります。
・良質な問題が多い
・手軽にアウトプットができる
・解説がついている
一見問題集は良さそうですが、私はあまりおすすめしません。
というのも以下のようなデメリットがあるからです。
(デメリット)
・全ての情報を暗記できているかを確かめられない
・理解していなくても始められてしまう
・やった気になりやすい
1つ目の「全ての情報を暗記できているかを確かめられない」ということについて説明します。
例えば「伊藤博文」について、1問1答の問題集では以下のような問題があったりします。
「ハルビン駅で安重根に暗殺された、日本の初代内閣総理大臣は誰?」
「答え 伊藤博文」
このような問題だと伊藤博文について、
・ハルビン駅で殺された
・安重根に殺された
・日本の初代内閣総理大臣
のいずれかを知っていれば答えることができます。
したがって、この問題に答えれたからといって、この3つの情報を全て覚えていることを確かめられません。
このように、生半可な知識・理解でも解ける場合があるのが問題集の怖いところです。
② 説明する
人に説明するのも立派なアウトプットです。
説明する方が、暗記への効果は高いです。
理由は以下のメリットの通りです。
(メリット)
・理解している証拠となる
・説明した全情報は暗記できていることが証明される
・質問されることで理解不十分なところが分かる
いきなりですが、理解には3段階あります。
説明を聞いたら分かる → 自分で問題が解ける → 説明できる
という3段階です。先ほどの問題集を解くというやり方だと、2段階目の理解までしか進むことができません。それに対し、説明をすることは、3段階目の理解まで進むことができます。
また「説明した全情報は暗記できていることが証明される」ということについては、
先ほどの伊藤博文を例にとると、
「伊藤博文は日本の初代内閣総理大臣として有名だけど、実はハルビン駅で安重根って人に暗殺されたんだよ」
と説明したら、伊藤博文について、
・ハルビン駅で殺された
・安重根に殺された
・日本の初代内閣総理大臣
の3つの情報を全て覚えていることの証明となります。
問題集と違って、生半可な理解・暗記じゃ説明はできません。
なので、説明は効果的な説明方法です。
しかし、以下のようなデメリットがあります。
・相手がいる方が良い
・全情報を網羅しているか判断できない
相手に関しては言うまでもないですね。
2つ目に関しては、例えば先の伊藤博文で言うと
「長州藩出身である」という情報を忘れていても、説明はできてしまいます。
これが説明の難しいところです。
③ 自分で問題を作る
そこで最後に私がもっともおすすめする方法が「自分で問題を作ること」です。
これは実際に私が行っていた勉強法で、ルーズリーフの左側に問題・右側に問題を書いていきます。
例えば、伊藤博文を例にすると、
「日本の初代内閣総理大臣は?」 「伊藤博文」
「どこ出身?」 「長州藩」
「どこで殺された?」 「ハルビン駅」
「誰に?」 「安重根」
といった具合です。
以下の写真は私が実際に書いた問題です。(大学の内容なので、少し専門的ですが・・・)

字が汚くて申し訳ないです。(笑)
この方法のいいところは以下の通りです。
・全情報をもれなく問題にできて、覚えているか確認できる
・自分が分かればいいので、問題文はフランクでよい
・問題を作れることは理解していることの証拠となる
このように、しっかりした理解が必要かつ網羅的な確かめができるのがいいところです。
「問題作ってから問題解くのきつい・・・」と思われるかもしれませんが、
問題を作っている時点で半分以上は覚えることができます。
問題を作ることもアウトプットなので、暗記の効果が高いです。
問題は紙に書いても良し、スマホに書いても良しです。
(個人的には紙がおすすめです。)
これを参考に自分に合った方法を見つけてください!
数学の勉強法についてもまとめていますので、以下をチェックしてください!









コメント